The Optics Of Rainbows

By Gustav Strömqvist | 

Rainbows are a beautiful physical phenomenon, forming as the result of how the sunlight refracts and reflects inside droplets of water before reaching your eyes.

In the visible range, water has a refractive index of n ≈ 1.33 or n ≈ 4/3, with a difference of around 0.0013, or 1%, between violet (400 nm) and red (700 nm). In the model shown here, n = 4/3 for λ ≈ 578.5 nm at T = 20 °C.

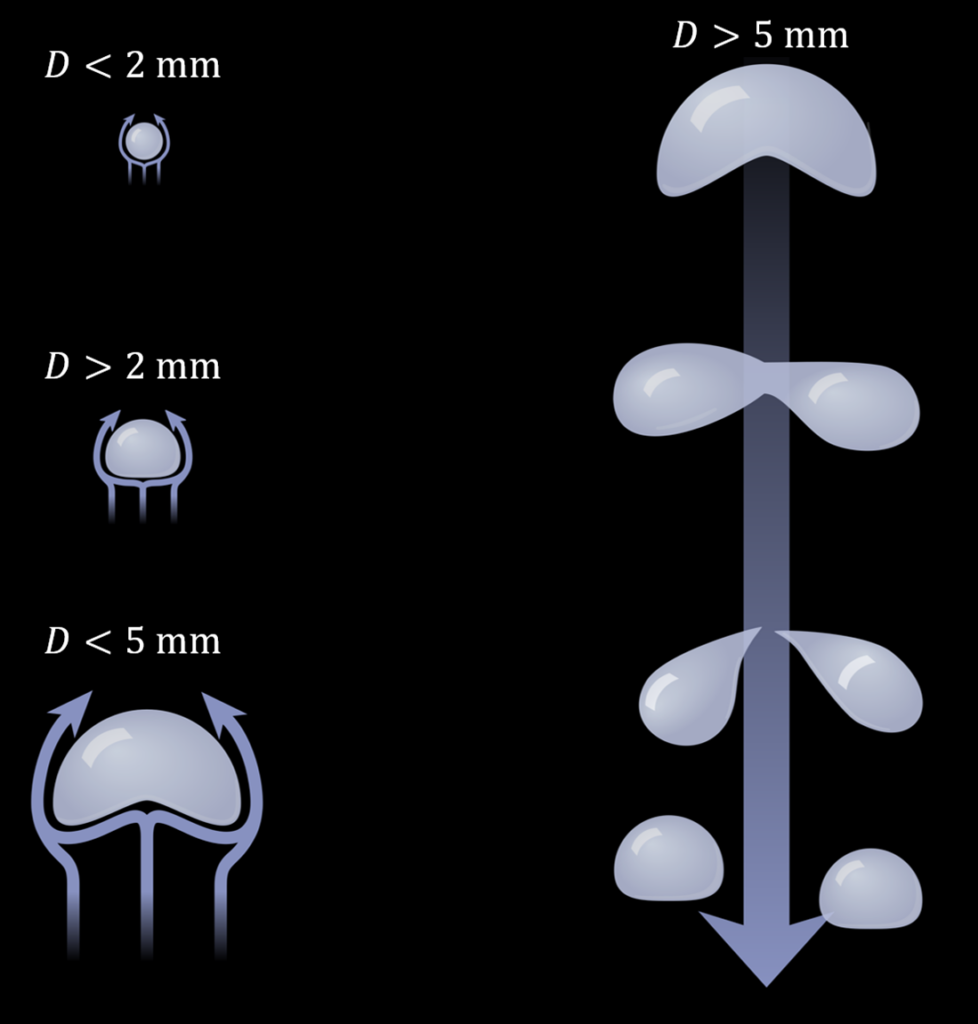
The physics of falling raindrops is not at all straightforward. Surface tension pulls the water towards a sphere, which is then flattened by air resistance towards a pancake shape. Larger drops eventually split into smaller ones. However, for drop diameters smaller than about 2 mm, the drops are nearly spherical, so we can approximate the rain as falling spheres of water, which greatly simplifies calculations.

We can then follow the path of a ray of light inside a spherical raindrop. A ray starts inside the sphere and hits the sphere with some angle of incidence, θ_w . When hitting the surface, the ray splits into a reflected ray with reflected angle equal to the incident angle, θ_w and a ray that is transmitted into the air with refracted angle θ_a = arcsin(n sin θ_w), provided that θ_w is smaller than the critical angle for total internal reflection, θ_c = arcsin(1/n), about 48.6°. Now the continuation of the ray path inside the sphere is simplified with the sphere approximation. Due to the symmetry of the sphere, the reflected ray has the same incident angle θ_w when it hits the sphere as the initial ray had. The incident and reflected angles in the sphere are always θ_w, and the refracted ray angle in the air is then θ_a after any number of reflections inside the sphere. All reflected and refracted rays lie in the same plane.

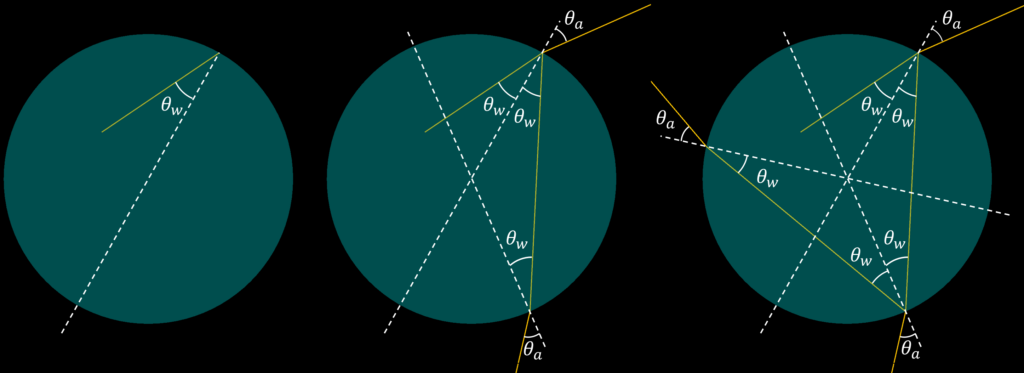
The light from the outside world could have any incident angle between 0° and θ_c ≈ 48.6° on the inside of the water sphere. Light with an incidence angle θ_w > θ_c could never leave the sphere, as we have seen that the incident angle is the same for all reflections. By the reversibility of ray optics, we can then conclude that a ray with θ_w > θ_c could not have entered the sphere from the surrounding air.

The figure below shows the light going to a sphere vertex on the horizontal symmetry axis. Here I did some cheating to avoid having to calculate the position on the sphere where a certain ray angle needs to hit to refract towards the chosen vertex. Instead, I used the reversibility of ray optics and traced rays from the vertex to the left at some angles to the horizontal axis between –θ_c and θ_c, with the limiting angles drawn as white rays in the figure. The rays refract out of the sphere to the left (reflected rays not drawn). Then I traced rays from the vertex at the same angles to the right, which refract out of the sphere to the right. We could now see it as if the light enters the sphere from the upper left (e.g. the fletched magenta ray), refracts into the water, hits the vertex and refracts out to the lower right, or reflects down towards the left to again refract out of the sphere. The magnitude of the angle to the horizontal axis for the ray exiting the sphere after one reflection is the same as for the ray entering the sphere, but it has been inverted. For a sphere, there is nothing special about the chosen vertex on the horizontal axis, so by rotating the entire figure, we could see how the light could go to any vertex directly after the refraction from air.

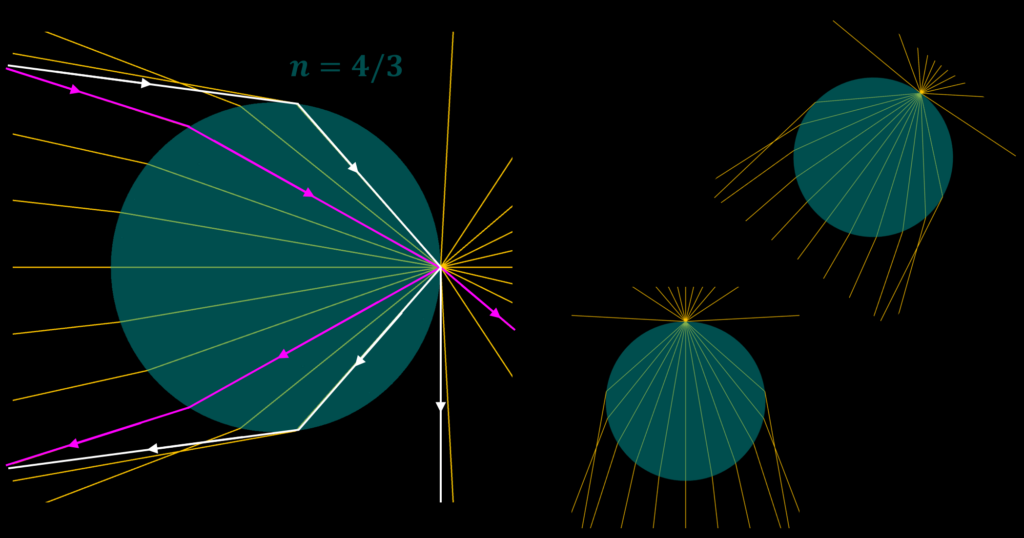
By denoting the ray angle to the horizontal axis by Φ, we see that the angle between the incoming ray and the ray exiting the sphere after one reflection is 2Φ. By looking at the angles between the horizontal axis and the radius going out to the point where the ray enters the sphere, it is found that the incident angle in air is θ_a = 2θ_w – Φ, leading through Snell’s law to the following relation between θ_w, Φ and n : Φ = 2θ_w – arcsin(n sin θ_w) where the allowed values for θ_w are between 0° and θ_c.

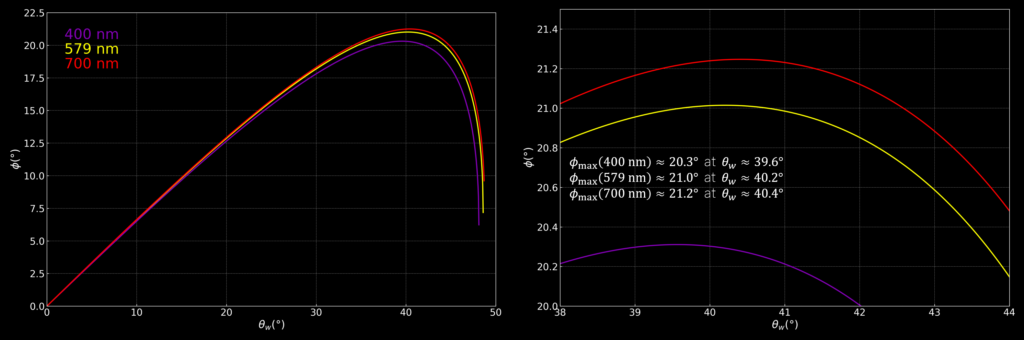
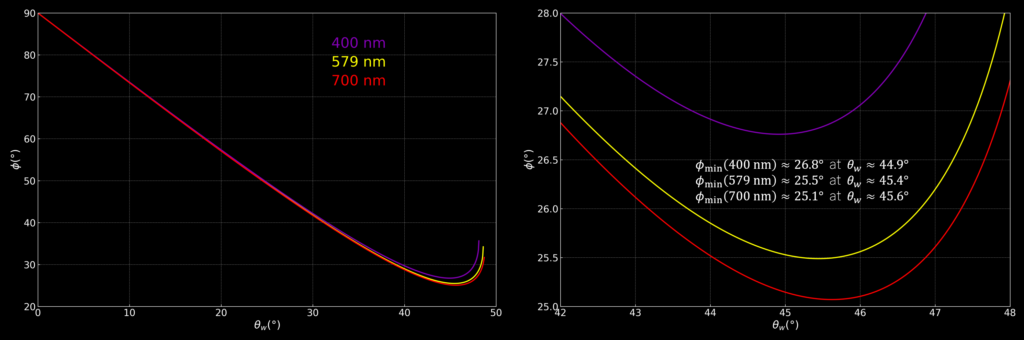
We can plot this relation for the allowed θ_w for different refractive indices (wavelengths). I here chose λ = 400 nm (n ≈ 1.342), λ ≈ 578.5 nm (n = 4/3), and λ = 700 nm (n ≈ 1.330). We see that each wavelength has a maximum Φ for some θ_w around 40°.

The distribution of the angular deviation of the light by the raindrop can be simulated by sending a large number of horizontal rays at random heights into the drop. By symmetry, it is sufficient to send light into half of the sphere, and we can choose to filter the outgoing light on the number of reflections inside the sphere.

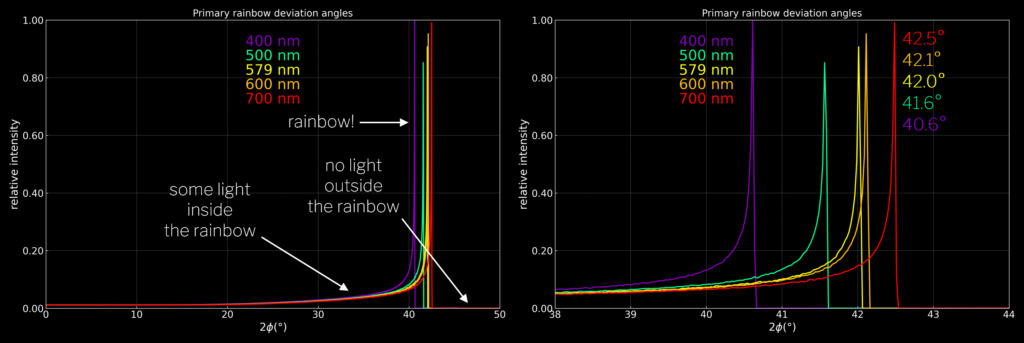
For one reflection, we get the following distribution of the relative intensity as function of the angle between the incoming and outgoing ray, 2Φ, for five wavelengths between 400 nm and 700 nm. We see that each wavelength has a sharp peak around its Φ_max and that there is some light for Φ < Φ_max, but no light for Φ > Φ_max. The visible colours have their peaks between 2Φ ≈ 40.6° and 2Φ ≈ 42.5° and this forms the primary rainbow with a peak-to-peak angular size of ~1.9°. The wavelength with the lowest refractive index (700 nm) has its peak where no other wavelengths can reach. Red colours should therefore be the most saturated colours in the rainbow.

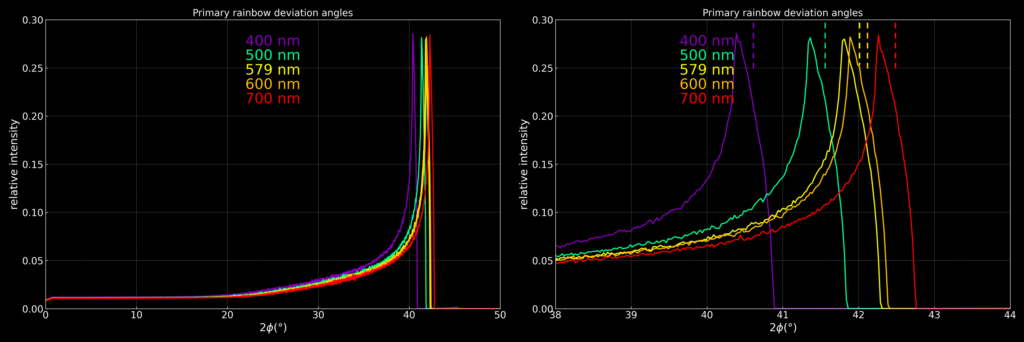
The simulation above was done with a sun that was a point source at infinity. The angular diameter of the sun is ~0.5°, which broadens the peaks and leads to less saturated colours. Due to the sharp edge around Φ_max, the peaks also shift by about half of the sun diameter. The point-source sun peak positions are marked with dashed lines to the right.

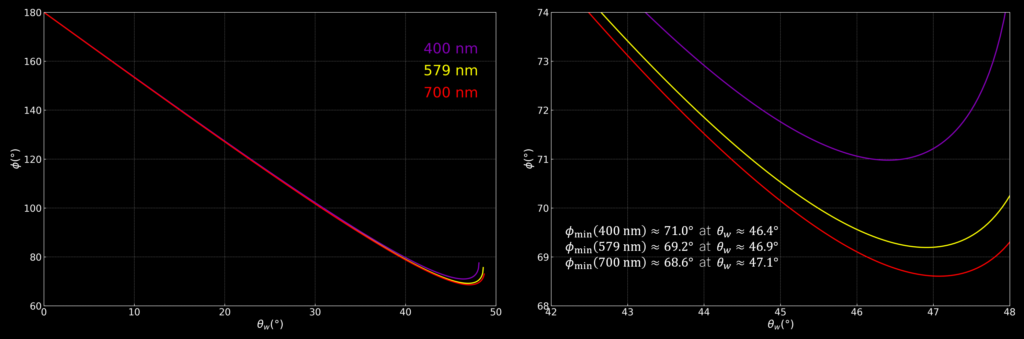
We can also look at the intensity distribution of Φ for another number of reflections inside the drop. For two or three reflections, the relations between Φ, θ_w and n are Φ = 90° – 3θ_w + arcsin(n sin θ_w) and Φ = 180° – 4θ_w + arcsin(n sin θ_w) respectively. For two reflections, each wavelength has its own minimum deviation angle.

For a point source at infinity, we get the following distribution of deviation angles 2Φ for the secondary rainbow. The visible colours have their peaks between 2Φ ≈ 53.5° and 2Φ ≈ 50.2° and this forms the secondary rainbow with a peak-to-peak angular size of 3.4°. The secondary rainbow is larger and weaker than the primary (same relative intensity scale in all plots) and the order of the colours is reversed.

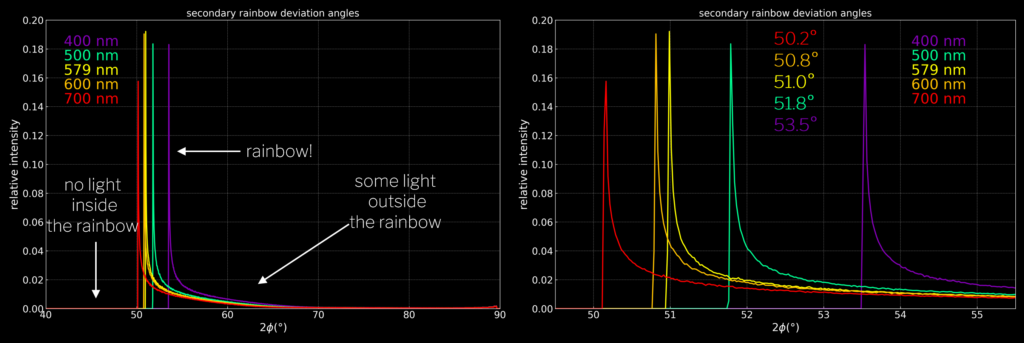
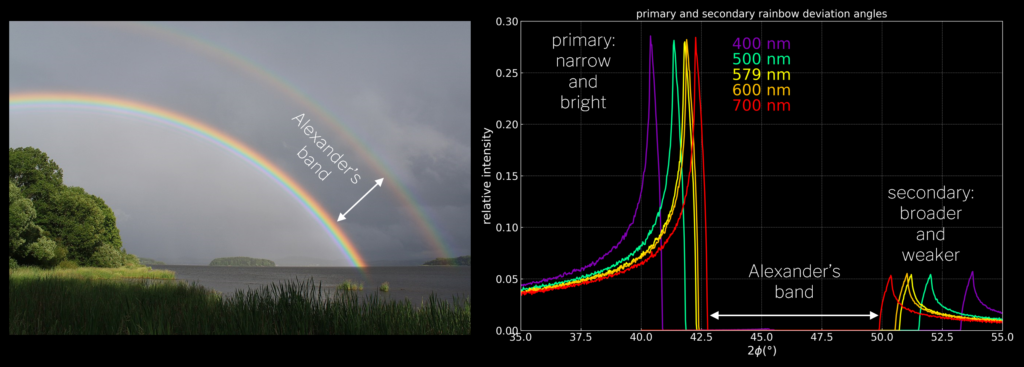
As there is some light inside the primary rainbow, but no light outside it, and some light outside the secondary rainbow, but no light inside it, a dark band forms between the rainbows from deviation angles of ~42.7° to ~49.9°. This is called Alexander’s band and is sometimes visible in photos, although it is more conspicuous that the inside of the primary rainbow is brighter than the outside. Below is a photo of a primary and a secondary rainbow and a simulation with an angular sun diameter of 0.5°.

For three reflections inside the drop, there is also a minimum deviation angle.

For a point source at infinity, we get the following distribution of deviation angles 2Φ for the tertiary rainbow. The visible colours have their peaks between  2Φ ≈ 141.0° and 2Φ ≈ 136.2° and this forms the tertiary rainbow with a peak-to-peak angular size of 3.8°. The tertiary rainbow is slightly larger than the secondary and is weaker.

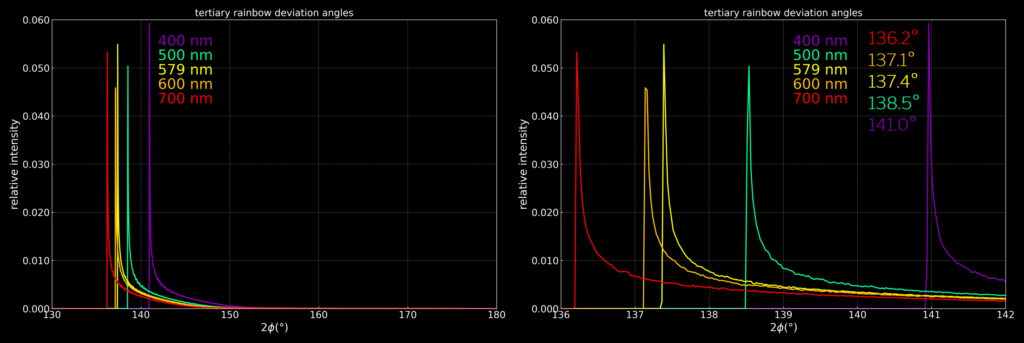
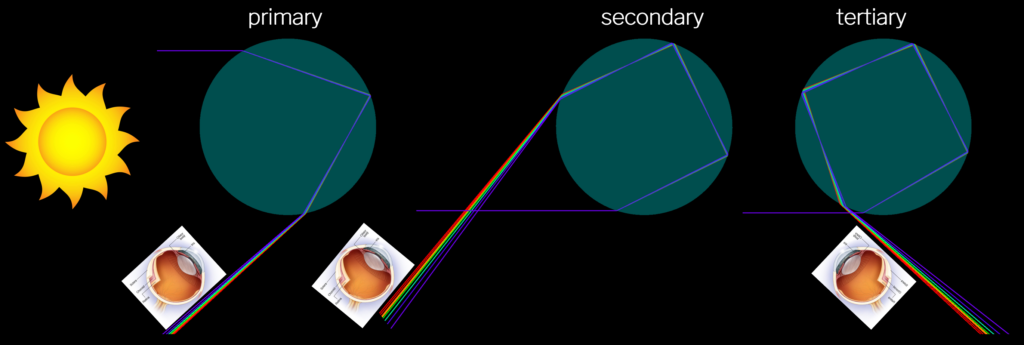
As 2Φ > 90° for the tertiary rainbow, it is located towards the sun at an angle of 180° – 2Φ ≈  52°.

I have not mentioned the possibility of a zeroth-order rainbow i.e. a rainbow that forms without any reflections inside the water sphere. The distribution of the deviation angles of light that is refracted into the water sphere and then refracted out without any reflections has no sharp peaks and is nearly the same for all visible wavelengths, meaning that there is no zeroth-order rainbow. However, the zeroth-order light covers a large angular interval, including that of the tertiary rainbow, and the two angular distributions are shown at the same relative intensity scale below.

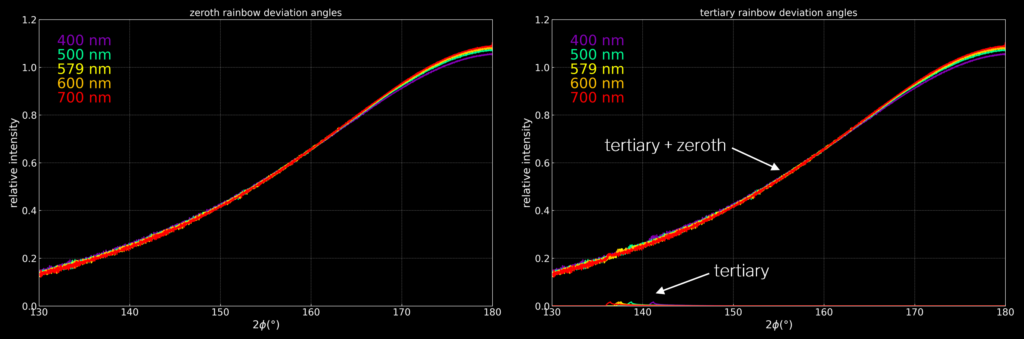
This means that it should be rather tricky to get a view of a tertiary rainbow, as it drowns in the zeroth-order background. If you manage to spot one, let us know!