The Myth of the 10 000 Lux Lamp

December in Stockholm and the sun rises at 8.30 and sets at 14.30, which makes many of us wonder, “why am I living here” or start looking for southern vacation destinations. It also leads to several articles in the newspapers about hacks on how to avoid winter depression or just get less tired. Artificial lighting is one way to do this, according to some sources.

What I often see in the health space is the incorrect use of irradiance when discussing these artificial lights. You often hear that “10 000 lux lamps” should be used. Which is something THAT DOES NOT EXIST!! [gasp]

A lamp or a source of light cannot have this property. Let’s start with the basics.

First of all, a source of light emits a certain total energy per unit time, which is called luminous flux and is measured in Lumen. Lumen is power (Joule/s) but scaled to the sensitivity of the eye. We are more sensitive to green than deep red so same power at these wavelengths will give a higher lumen value for green.

Next, the light from the source has an angular distribution , and if the light is emitted in a small angle the source will appear much brighter than if it is more spread out. The emission angle is measured in steradians, which is a 2D angle. The flux per space angle, the Luminous intensity, is measured in lumen/sr or candela. One (1) candela corresponds to one single candle!

Thirdly, a source may have different sizes. A large source that emits light over a certain angle will appear less bright than if the same amount of light came from a small source area. So therefore, the proper way to characterize a light source in the visible range is by Luminance. Luminance is measured in lumen/ m²/sr or candela/ m² and is therefore a great way to characterize a source. Luminance is constant with distance and relates to the perceived brightness (although brightness is not constant for all distances [ref1]). There are many other names and units for this quantity (my favorite is foot-lambert), you can find them on Wikipedia. There you can also find a great example of a candlelight, showing how the luminance can vary over the source area.

https://en.wikipedia.org/wiki/Luminance

Lux on the other hand, is the measurement unit for the amount of light radiated onto a surface and is called illuminance. Lux can also be written as lumen/m². Since Lumen is the same as power, lux is power per illuminated area. Obviously not a source property. For a given source of light, with a given Luminance, the illuminance will depend on the distance to the light source since light is often spreading out (even a laser).

So why is it called a 10 000 lux lamp? I think the reason is partly due to the lighting industry, which misuses lux values to compare their sources, since illumination after all is the basic use for light sources. You are more often looking at a surface that is illuminated, rather than at the source. But the lighting industry uses a standard distance for this, often 1 m. This is however not that case for the therapeutic lamps.

So, what about my winter fatigue? Before we go into this, we need to discuss one more parameter – the spectrum! The spectrum matters and it is very different depending on the source.

Let’s have a look at the solar spectrum (which is really not smooth) and compare it to incandescent and fluorescent light:

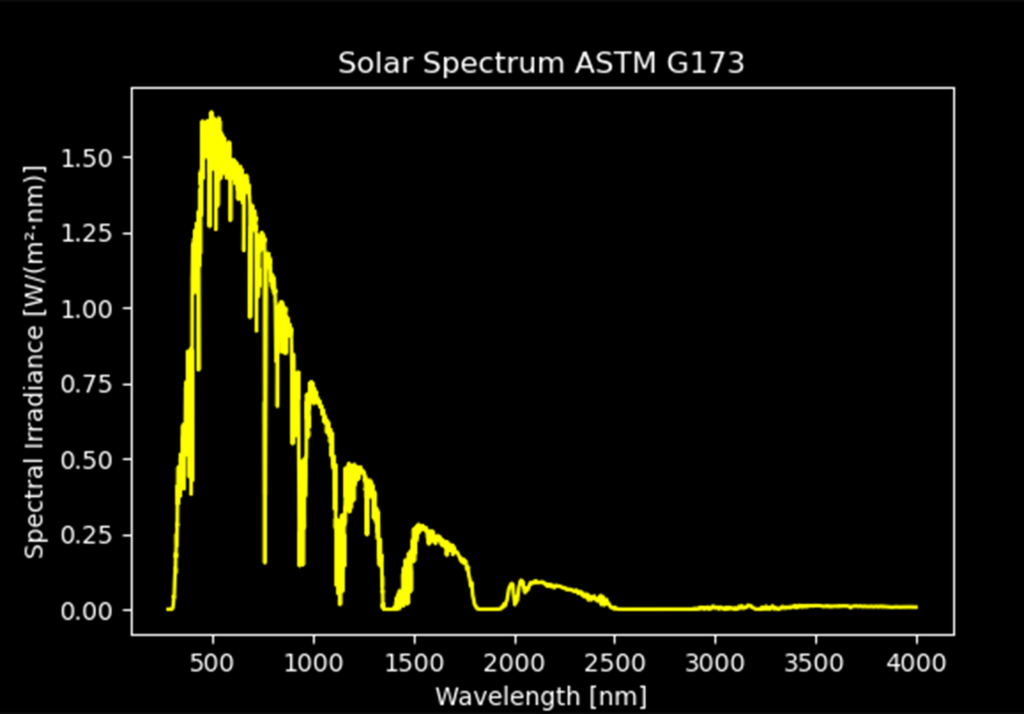
This sunlight spectrum is based on a standard called ASTM G173 which is an average measurement of direct sunlight under moderate incident angles (48.2 degree solar zenith angle). The irradiance corresponds to 100 000 lux, which equals direct sunlight on a clear day.

You can get a full description of this data here: https://store.astm.org/g0173-23.html And now the spectra from incandescent light and a fluorescent light source:

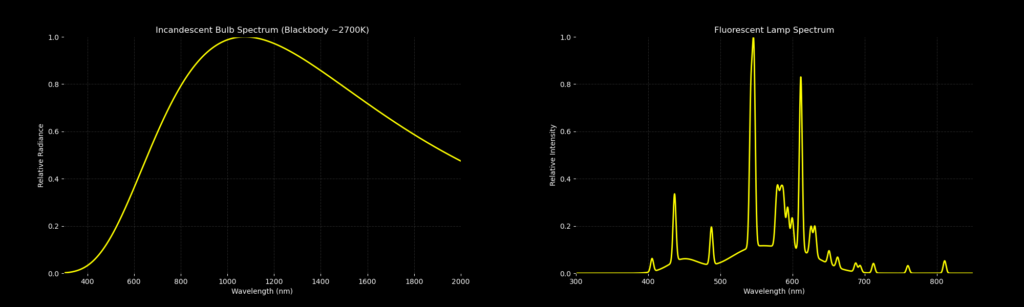
Certainly, the fluorescent light is REALLY not smooth nor possible to match to the solar spectrum. Also, you can see that a major part of the incandescent light lies outside of the visible spectrum. Now, some research seems to show that this long-wavelength light is good for us (maybe more on this in a different post), so maybe light in this part of the spectrum  is not waste when it comes to health benefits but it is not contributing  to the illuminance, since this is scaled to the photopic response of the eye. The photopic response curve looks like this (cred to Wikipedia, https://commons.wikimedia.org/wiki/File:CIE_1931_Luminosity.png):

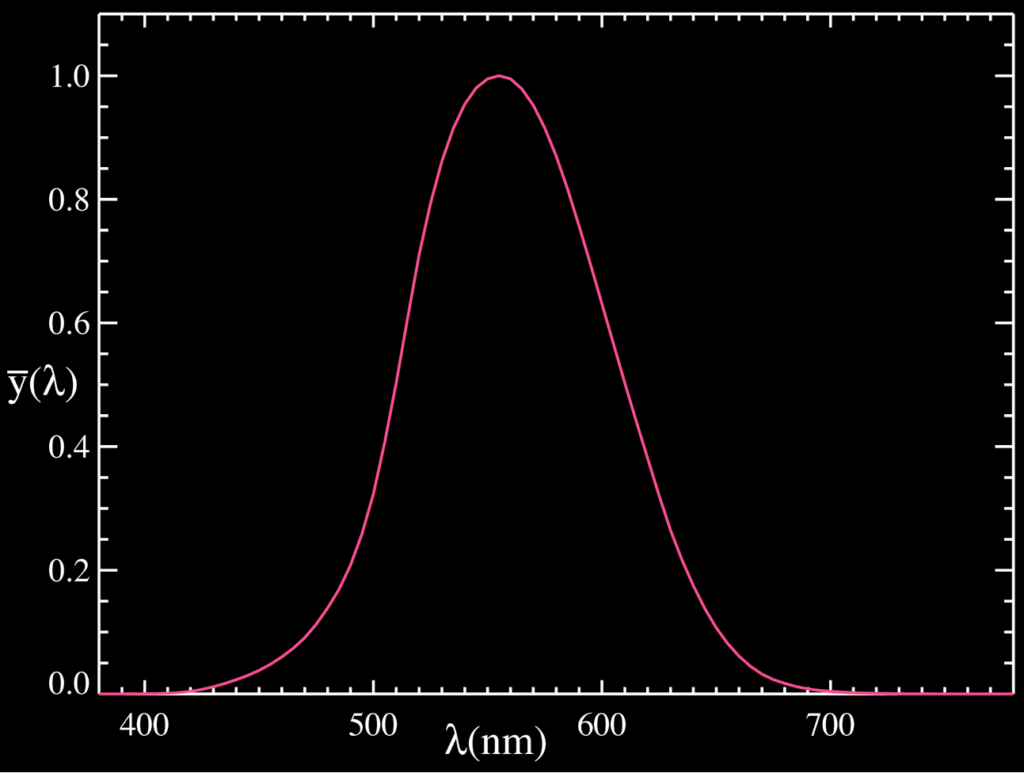
In order to go from irradiance to illuminance we need to integrate the product of this photopic response curve V(λ) and the light source,

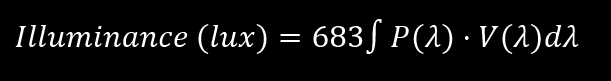
With the irradiance P(λ) and V(λ) is the photopic response curve. One often sees this integration as a scale factor, called the luminous efficacy. With the luminous efficacy you can go between irradiance and illuminance for a given source, but the value is given by the above integration.

OK. So back to the 10 000 lux lamp that will hopefully help me during the winter months. Where does the number come from? The 10 000 lux lamp seems to originate from studies in the 80s and 90s showing that 10 000 lux at eye level is a safe and reliable way of using artificial light in order to establish and maintain circadian rhythm and treat SAD (Seasonal Affective Disorder) when there is low or no natural sunlight in the mornings (like here in the Nordic countries). In these studies, they used fluorescent lamps.

As we see above, the fluorescent lamp has a spectrum very far from the solar spectrum. But how about if we try and match the sun spectrum with an incandescent bulb. At least part of it? It would look something like this:

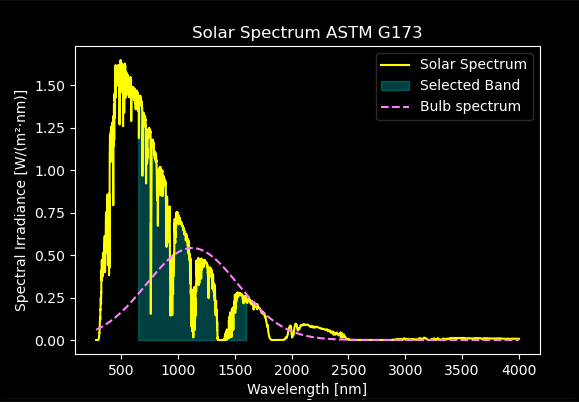
In the waveband highlighted in the figure, the integrated irradiance is 489 W/m². If we have a 50 W lightbulb and want to achieve this irradiance, (assuming uniform angular spread and a point source) it will need to spread over a sphere with a radius of 0.09 m. That is quite close! However, we were aiming for lux so we need to switch to  illuminace. Calculating the luminous efficacy for this source we get 41 lumen/W, which yields 20 000 lux at 0.09 m and 10 000 lux from the incandescent bulb would be achieved at 0.13 m. That is doable!

If we instead use an LED? White LEDs typically have a high peak in blue and a long tail from the fluorescence, depending on the color temperature. For a cold LED the matching could look something like this:

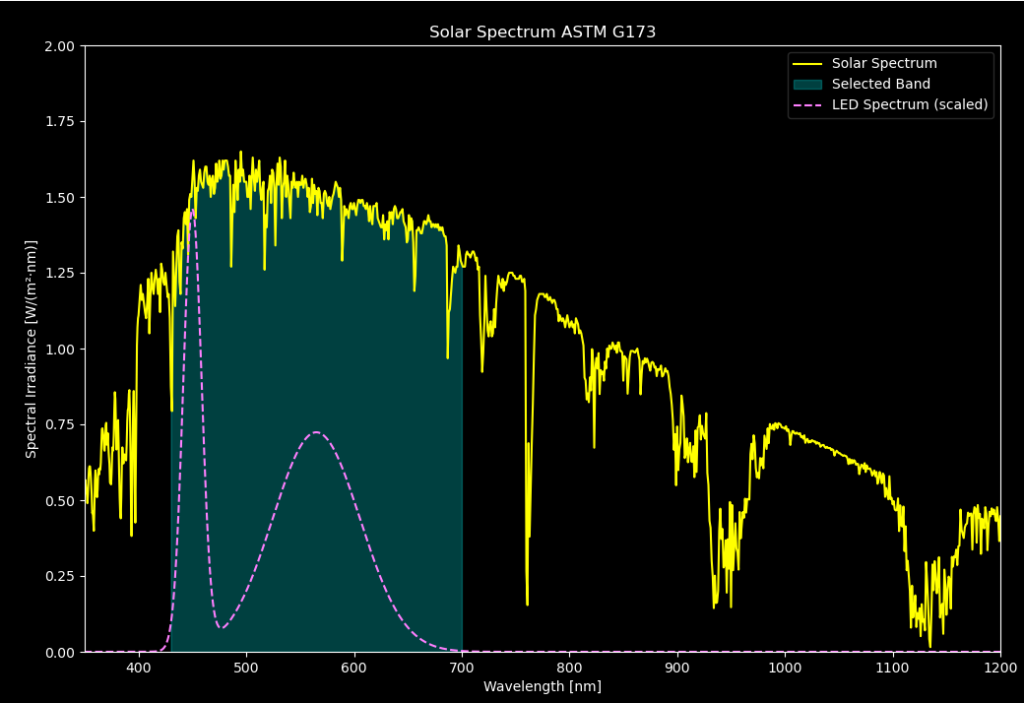
In this waveband (450 nm – 700 nm) of the solar irradiance there is 425 W/m2 (out of total 1000 W/m2). If we want to achieve this irradiance level with an LED with Lambertian light distribution  (half power angle equal to +/- 60 degrees) with 1 W output, we need to be 27 mm from the LED (bit more complicated calculations here). Now if we again convert this into illuminance, using the spectrum above, the illuminance we get is 184 000 lux! Mamma mia! This may seem counterintuitive, but we are concentrating light from a wide spectrum and pushing it into two peaks which are much more visible to the eye.

184 000 lux may seem a bit too much. If I want 10 000 lux from a white LED, we can increase the distance to 120 mm. The illuminated area from my 1 W Lambertian LED at this distance is 0.4 m before dropping to half of the peak value, good enough to cover my face!

If you want to build your own LED 10000 lux lamp, or just calculate the irradiance from the sun in a certain waveband, you can use this online calculator. Right now you can only use gaussian spectrums, but just drop me a note and you can get the python file or loading and making your own spectrum.

Here is how it works: 1) Enter the wavelength band for the solar spectrum where you want to integrate, then press “Integrate over waveband”. The result is shown above the graph, where also the waveband is highlighted. 2) Enter the data on the LED, the full width half maximum angle of the angular emission and the total power. 3) Press “Calculate LED distance”. The calculator calculates at what distance the peak irradiance will match that of the sun and also provides the peak illuminance value on a flat surface. If you want to change the illuminance, you can lower the input solar illuminance, by changing it from its default value of 100 000 lux.

Follow this link to use the calculator: https://eclipseoptics.com/solar-irradiance/

Have fun and thank you for reading!

References

[1] Ronian Siew 2008 Eur. J. Phys. 29 1105 ”Corrections to classical radiometry and the brightness of stars”